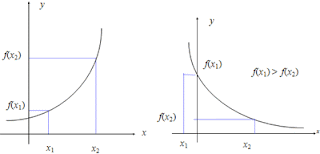
La derivada es El limite del Cociente del Incremento de la variable Dependiente Entre El Incremento de la variable de los independientes, Cuando Este Tiende un cero, lim -> 0: ^ y / ^ x.
REGLAS BASICAS
1. Constante para una "a":
Si f (x) = a, es Su derivada f '(x) = 0
Ejemplo: Si f '(x) = 16, es derivada Su f' (x) = 0.
2. Para una suma de Funciones:
Si f (x) = u (x) v + (x), es Su derivada f '(x) = u' (x) + v '(x)
Ejemplo: Si f (x) = 3x2 + 4x, es derivada Su f '(x) = 6x + 4.
3. Regla de Producto
Si "u" y "v" Los polinomios hijo:
La funci0n: f (x) = uv
Su derivada: f '(x) = uv + u'v'
Ejemplo: f (x) = (6) (15)
f '(x) = (6) "(15) + (6) (15)»
4. Regla del Cociente
This Regla es util en sí de Cuando Tiene Una funcion formada de la división de polinomios.
Si "u" y "v" Los polinomios hijo:
La funcion: f (x) = u / v
Su derivada: f '(x) = u'v - uv' / v2
Ejemplo: f (x) = 2x3 + 3/3x4 - 5
f '(x) = (6x2) (3x4 - 5) - (2x3 + 3) (12x3) / (3x4 - 5) 2
5. Regla de la Cadena
This Regla es util en sí de Cuando Tiene Una funcion formada Por Un polinomio un Elevado Una Potencia.
Si "u" El polinomio es:
La funcion: f (x) = sin
Su derivada: f '(x) = n (u) n-1 (u')
DERIVADA DE ORDEN SUPERIOR
En Ocasiones ALGUNAS es Necesario Calcular la derivada DE UNA derivada; hijo ESTAS Llamadas derivadas de Orden superior.
Para determinar Una derivada de Orden superiores en sí un proceder Calcular la derivada de primera, luego! Sí cálculo la derivada de la derivada de primera, sí Con la continua derivada de la Segunda y asi sucesivamente derivada Hasta Llegar a la derivada Deseada.
La notacion comun UTILIZADA párr Las derivadas de Orden superior es la Siguiente:
* Primer derivada dy / dx = f '(x) = y'
* Segunda derivada d2y/dx2 = f''(x) =''y
* Tercera derivada d3y/dx3 = f'''(x) =''y'
* Cuarta derivada d4y/dx4 = f (4) (x) y = (4)
* Enesima dny derivada / dxn = f (n) (x) = y (n)